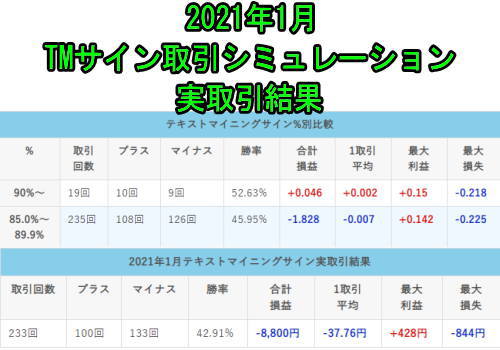
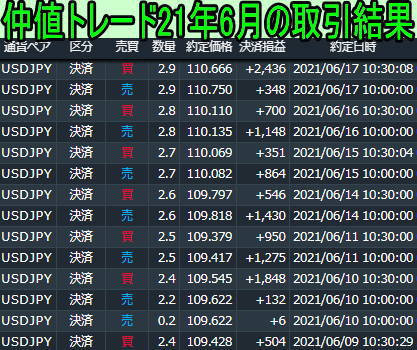
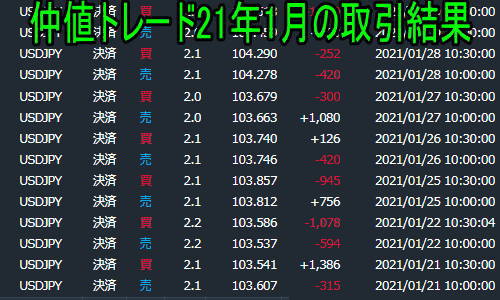
今日はケリー基準(ケリーの公式)を使って、期待値が同じでも確率が変わると投資対象の価値が変わるのを確認したときの記事を投稿します。
※ケリー基準(ケリーの公式)を正しく理解、解釈しているか分かりませんので参考程度でお願いします。
ケリー基準(ケリーの公式)は、資産の何%の資金量を投じるのかを判定してくれる計算式です。
ギャンブルや投資など不確実性のある状況において収益を最大化する資金配分を導く経済学の法則であるケリー基準(Kelly criterion)の発見で知られる。
引用元: ケリー基準
※ケリー基準(ケリーの公式)を使うときは張りすぎを起こすときもあるみたいなのでご注意ください。
計算式
ケリー基準(ケリーの公式)の計算式です。
f=(p×(b+1)–1)÷b
- f=資産の何パーセントを賭けるべきか
- p=確率
- b=オッズ(US方式)
オッズは、増えた分の数値になります。
例:3倍の配当だった場合、1を掛けて産の配当なので、入力する数値は3ではなく2になります。
見た目難しそうですが、確率とオッズを入力するだけです。
期待値±0の場合と式の確認
ケリー基準(ケリーの公式)を理解していない可能性があるので、いくつか入力して確認してみました。
丁半博打のように確率1/2でオッズが2倍のような期待値が±0のような場合
- 資産の何パーセントを賭けるべきか
0.00% - 期待値
0

期待値0の投資先には投資をしないという事ではないかと思います。
確率を100%に変えて検証
なかなか現実にはない条件になりますが
確率を100%に設定してみます。
- 資産の何パーセントを賭けるべきか
100.00% - 期待値
1

それそうですよね。100%の確率で勝てるのであれば全財産を投資しますよね。
ただ、現実にこのような条件があると逆に怖くて全財産を投資できないです^^;
確率は100%のまま期待値を1.001(0.1%)に設定してみます。
- 資産の何パーセントを賭けるべきか
100.00% - 期待値
0.001
どんなに期待値が下がっても、100%の確率であれば全財産を投資すると判断しました。
自分のように財産が少ない場合は、無理して投資しなくていいのでは?とも考えてしまいますね。

確率を下げて検証
オッズを2に戻し
確率を90%に設定してみます。
- 資産の何パーセントを賭けるべきか
80.00% - 期待値
0.8

そのほかを試すと期待値と掛け%が同じということが分かりました。
オッズを2
確率を80%に設定

オッズを2
確率を60%に設定

適当に変更して期待値を0.8に合わせると、期待値と掛け%が同じではない。ということが分かりました。


ここで期待値が同じでも確率が変わると掛け%が変わるということが分かりました。
また、こちらのサイトの計算機で計算したのと数値が同じになるので計算自体は合っているのが確認できました。
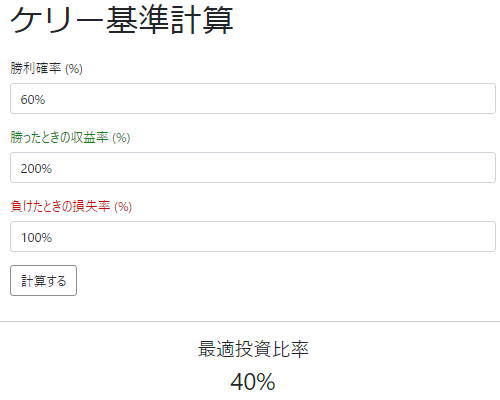
グラフも表示されるので分かりやすいですね。
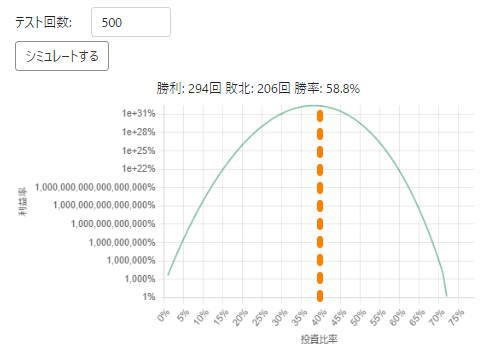
身近な数値で計算
ここまでは計算方法があっているのか確認したかったので極端な数字を使いましたが
ここでは現実的な数値に変えてみます。
確率50% オッズ2.1
確率を50%にしてオッズ2.1で計算してみると
- 資産の何パーセントを賭けるべきか
4.55% - 期待値
0.05

イメージとしてはこのような感じです。
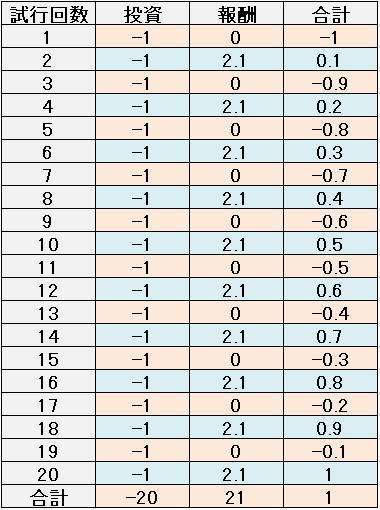
投資期間にもよりますが、この辺の数値で投資できるといいですね。
期待値が同じで確率が違う場合の比較
さきほど出した数値と
確率を下げ、オッズを上げ、期待値を同じままの数値で比較してみます。
確率を5%にしてオッズ21.0で計算してみると
(左が50%右が5%)
- 資産の何パーセントを賭けるべきか
0.25% - 期待値
0.05

4.55%から0.25%へ下がりました。
イメージとしてはこのような感じです。
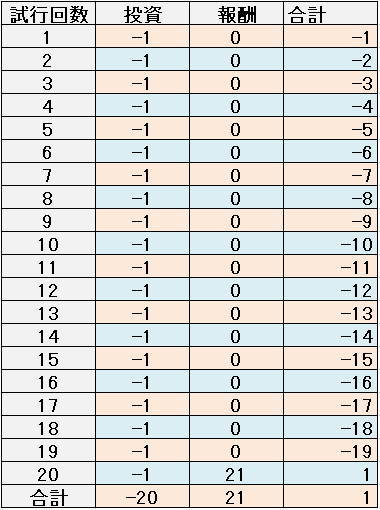
最後に
※ケリー基準(ケリーの公式)を使うときは張りすぎを起こすときもあるみたいなのでご注意ください。
収束するまでの試行回数が増えるので投資額を減らすというのは、なんとなく分かっていましたが、ここまで極端に下がるのにびっくりしました。
それよりも、期待値が0のときに掛け%が0%という数値を見て、0%に近づくにつれて投資価値が低いという”ものさし”にもなると解釈できました。
これはFXと関係ない話になってしまうのですが、以前働いていたころ週末に副業でパチプロ(スロット)で稼いでいました。
この時に”期待値”という言葉が飛び交っていて、勝率は考慮されず期待値は少しでも高い方が良いと解釈されていました。
この計算方法を見て数年ぶりにすっきりしました^^
具体的な台で言うとハーデス、凱旋の天井狙いとサラ番、まどマギのゾーン狙いです。
競馬で例えると、馬単と3連単でしょうか。
収束させられるまで時間もかかるので収束する前に破産してしまう可能性もあり、永遠に投資機会が訪れるとも限りませんので確率は重要だということが確認できる計算式だと思いました。
[gads]